TCC home About TCC Site Map Contact us

Guidance Tool Usage

Advantages of tool utilization

• The tool is a JMA web-based application accessible via a web browser with no need for additional software or plug-ins.
• Users need to provide only past observation data to create guidance forecasts. Past and real-time forecast data are stored on the application side.

Provision of past observation data

• Element: daily temperature or daily precipitation
• File format: CSV (comma-separated values)
• Period: As a minimum, daily data covering the verification period (from 1 January 1991 to 31 January 2021 by default) are required.
• Metadata-like elements for certain types of information on observation points should be described in the first five lines as below. Be sure to add "#" at the beginning to indicate a comment line. An undefined value can be set on the second line (#undef).
• A station name should be just one word. In case of more than one word, connect with hyphen "-".
• From the sixth line onward, the date and observation data should be listed in the form "year,month,day,value". Undefined values can be used for missing data. For precipitation data, use "0.0" for rainfall values less than 0.1 mm. Refrain from using character strings such as "Trace" and "T".
• Guidance forecast information can be created simultaneously for up to 10 observation stations.
  
  #elname=temperature,,,  → "temperature" or "precipitation"
  #undef=-9999,,,  → undefined value in case of missing data
  #station=,,,TOKYO,NIIGATA,SENDAI,NAGOYA,OSAKA,SAPPORO,HIROSHIMA,TAKAMATSU,FUKUOKA,NAHA  → station name (up to 10 stations)
  #lon=,,,140,139,140.8,137,135.5,141.2,132.5,134,130.4,127.6  → longitude of the station
  #lat=,,,35,38,38.25,35.2,34.6,43,34.4,34.3,33.5,26.2  → latitude of the station
  1991,1,1,6.6,6.6,6,8.2,11,-0.3,10.8,9.9,12.3,21
  1991,1,2,7.9,6.5,6.5,9.5,10.9,0.2,10,9.9,8.7,18
  1991,1,3,8.3,2.4,2.2,6.8,7.4,-4.6,5.7,6.3,5.1,17.4
  ....
  
  
• Observation data sample in Japan: Temperature, Precipitation

In-browser parameter settings

• Set the desired value for "Initial date." The relevant values for "Forecast period" (the start and end dates) will automatically appear in the next pull-down column.
• Set "Forecast period" to create a guidance forecast. Select the date with the range between the start and end dates of the target period.
• Set the desired "Predictor" elements from the pull-down menu. Up to three elements can be input starting from the left (Nos. 1∼3).
• Upload the relevant past observation CSV file.
• Click "Submit."

Figures and data

• After background calculation, four figures will appear on the screen.
• The upper-left figure shows a tercile probability map for the selected forecast period.
  Warm- and cold-colored markers denote warmer- and colder-than-normal values for temperature forecasts, respectively.
  Green and orange markers denote wetter- and drier-than-normal values for precipitation forecasts, respectively.
• The upper-right figure shows tercile probability (color bars) at stations.
• The lower-left figure shows an inter-annual time-series representation of tercile probability for the verification period (cumulative bar chart) at stations.
  Coefficients of correlation for two or three selected predictor elements are displayed on top of the figure to allow checking for possible predictor multi-collinearity (see Predictor combination and multi-collinearity issues for details).
• The lower-right figure shows a reliability diagram with reliability (red lines) and forecast frequency (green bars).
  Brier skill score (BSS), anomaly correlation coefficient (ACC) and Akaike's information criterion (AIC, see Appendix) data are also shown in the figure.
• The CSV-format data file used to create the figures (with information such as probability, coefficients and constants of the regression model, observation and forecast values, and reliability information) can be downloaded by clicking the "Download CSV file" link at the bottom of the screen.

Sample temperature probability forecast map for each category. Cool-, grey- and warm-colored marks denote below-, near- and above-normal probability, respectively.	Sample temperature probability forecast for three categories. Blue, grey and red bars denote below-, near- and above-normal probability, respectively.
Sample temperature probability forecast for three categories. Blue, grey and red bars denote below-, near- and above-normal probability, respectively. Black and green lines are inter-annual timeseries representations of daily-mean observation and forecast anomaly data, respectively.	Sample reliability diagram. Red lines show reliability and green bars show forecast frequency.

Detailed Options

• Click "Detailed options" to change the variables listed below as desired for guidance forecast creation. It is advisable to keep the defaults unless there is a particular need to change them.
• Verification period: The period can be adjusted to avoid inappropriate times during which large amounts of data are missing. The default is the 30-year period from 1991 to 2020.
• Station name character size: The station name character size in the figure on the upper left can be changed. The default is 0.09.
• Normalization of precipitation data: The power value used to normalize precipitation data can be adjusted. The default is 0.25 (1/4).

Basic Concept of Numerical Guidance

Outline of MOS guidance

• Numerical guidance is provided to support translation of model output values into targets of forecasting. Its principle involves the prediction of future values based on statistical relations using model forecasts and observation data from past cases. To determine these relations, an extensive time-series representation of past forecast data generated by a consistent forecast model (known as a hindcast) is necessary.
• If the climate is relatively stable, errors from past similar cases can be used to statistically correct the current numerical forecast (e.g., biases included in hindcast datasets can be used to reduce biases in current numerical forecasts).
• This approach is widely known as guidance provision, and is based on model output statistics (MOS).

Objectives of guidance

• Support clarification of the effects of sub-grid scale topography (model output may not reproduce the effects of local topography due to limited resolution) while enabling large-scale field reproduction.
• Reduce model imperfections such as systematic bias errors.
• Enable estimation of degrees of uncertainty in consideration of prediction skill.
• Guidance provision helps to improve prediction skill as compared with direct model output.

Data and method

• Time-series data from past observations and previous model forecasts (i.e., hindcasts) are used to produce guidance.
• Statistical relations are estimated using these two data types for the verification period (30-year period from 1991 to 2020 by default). The results are used to calculate current values in real-time forecasts.
• As the locations of observation stations and equally spaced grid points generally do not correspond, forecast and hindcast data are spatially interpolated using the four neighboring grid point values.

Regression model Multiple linear regression modeling is used for statistical prediction based on past forecasts for the statistical period. In such modeling, the predictand Y is related to the N predictors Xi. The predictand is estimated from a linear combination of predictors. Here, ai represents the regression coefficients, b is the regression constant and ε is the error term. The coefficients ai and the constant b are determined such that the sum of the squares of estimation errors is minimized. The analysis procedure is detailed below. 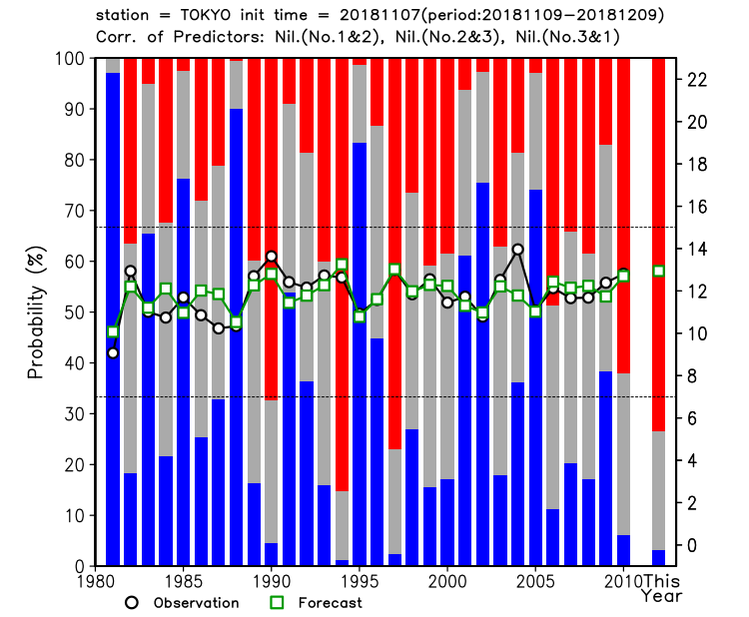Calculation of the factors ai and b is based on past observation data variables such as temperature and precipitation and on past forecast (i.e., hindcast) elements for the same period from the verification period (30-year statistical period (1991 - 2020) by default). Prediction of objective variables from real-time forecast elements multiplied by these factors is conducted using the relevant simultaneous equation. 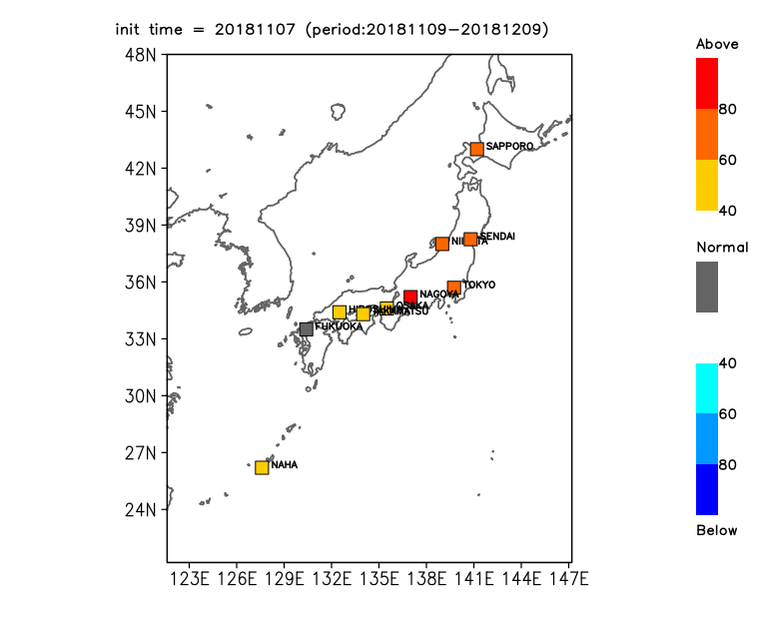Mapping from the objective variable to three categorized forecasts based on the ranking is conducted. 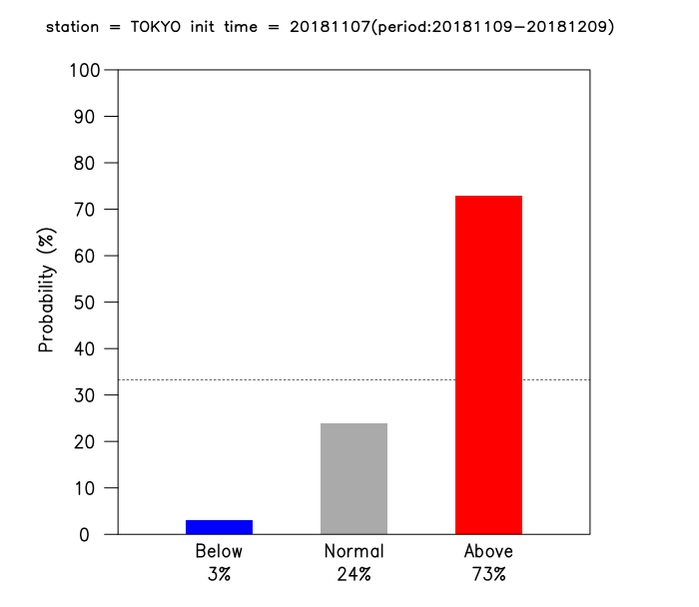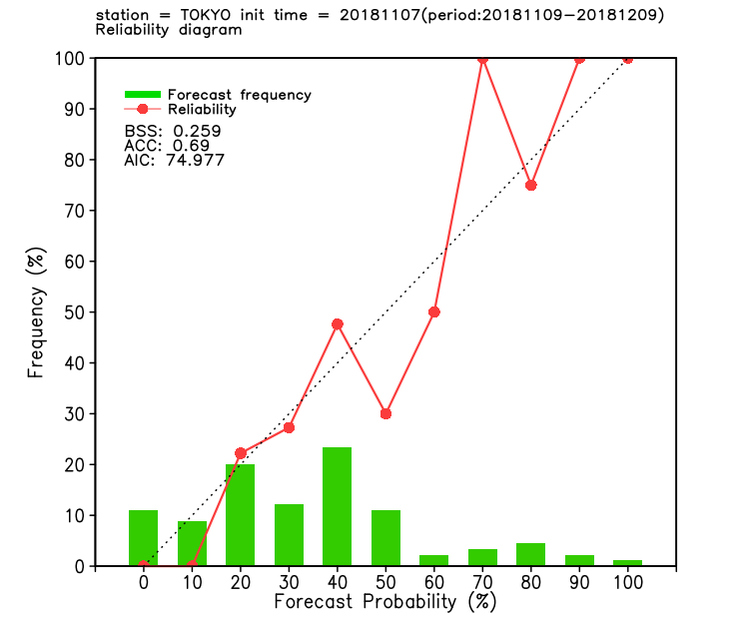In the guidance tool, the probability density function (PDF) is assumed to have normal distribution. Here the mean (xs) is a prediction value from the regression model and the standard deviation (σn) is the error of the model, assumed to be its RMSE based on hindcast data. Threshold values for the three categories are determined from past observation for the verification period (from 1991 to 2020 by default). Probability for each tercile category (below-, near- and above-normal) is calculated with reference to the PDF of guidance and the threshold values for the three categories. The cross-validation technique (Bishop 2006) is not used to create the regression model.

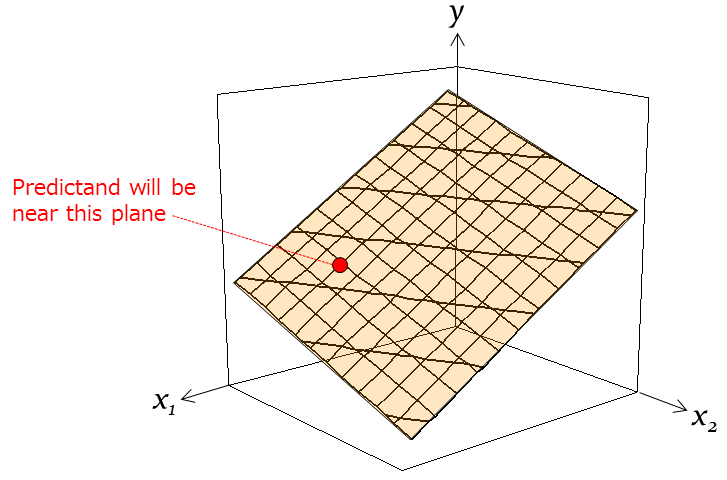
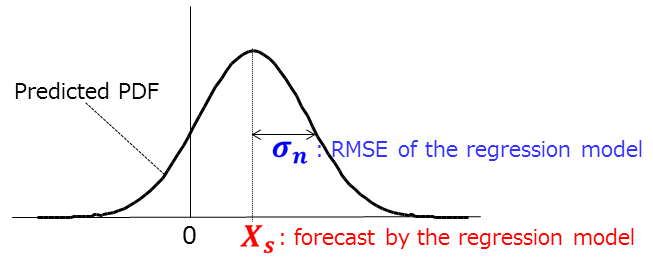
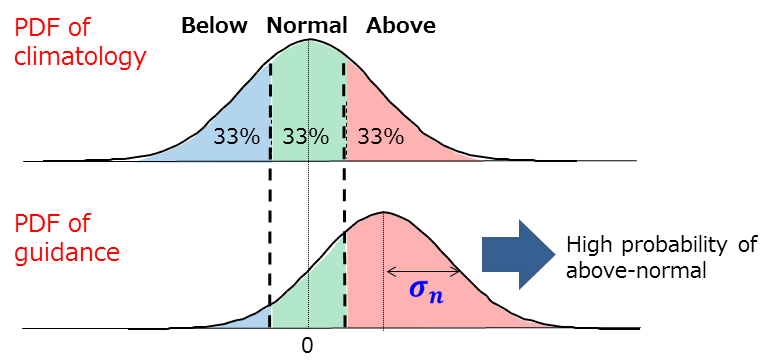
Conceptual diagram for a linear regression model of the predictand y and two predictors (x1 and x2). Sample of predicted PDF with normal distribution. xs and σn denote the mean forecast and the standard deviation, respectively. Sample climatorogical and predicted anomalous PDF for guidance forecasting.

Normalization of precipitation data Normal distribution is assumed in the regression model. Temperature distribution is generally approximated as per the normal. Precipitation distribution is generally approximated as per the gamma equivalent rather than the normal. For approximation based on normal distribution, the guidance tool performs normalization of precipitation data to the power of 1/4 by default.

Predictor combination and multi-collinearity issues

• For temperature forecasts:
• Setting of one predictor among temperature-related elements (such as lower-tropospheric or surface temperature) is recommended.
• Predictors other than temperature-related elements (such as wind components) should also preferably be set.
• For precipitation forecasts:
• Setting of one predictor among moisture-related elements (such as rainfall or relative humidity) is recommended.
• Predictors other than those depending on regionality (such as lower-tropospheric wind) should preferably be set in consideration of terrain conditions.
• Multi-collinearity is a material issue in multiple regression analysis. It relates to the presence of an explanatory variable combination with a significantly high correlation, causing poor forecast results. To prevent multi-collinearity, setting of poorly correlated predictors is recommended. Coefficients of correlation coefficients between selected predictors can be checked in the lower-left figure.

Over-fitting issues

• With smaller or larger sample sizes, coefficient variation in the multi-regression model tends to be larger or smaller, respectively, in association with the number of predictor elements, and coefficients that are unstable or stable, respectively, are obtained. This is referred to as over-fitting (Bishop 2006).
• It should be noted that selection of multiple predictor elements will not necessarily lead to improved multi-regression model forecasts.

Verification for probabilistic forecasts

Reliability diagram Reliability curve (red line): Plots observed frequency (Y-axis) against forecast probability (X-axis). Proximity of the reliability curve to the 45° line (perfect reliability) represents better probabilistic forecast results. Forecast frequency (green bar). Forecast scores The Brier score (BS) indicates mean squared error of probability forecasts. BS values can be referenced in the downloadable CSV-format file. Here N denotes the sample number (i.e., over a period of 30 years), m is the probability category, pim is the forecast probability and oim is the outcome (1 for occurrence, 0 for non-occurrence). BS values range from 0 to 1, with 0 being a perfect forecast. The Brier skill score (BSS) indicates skill relative to a reference forecast (usually climatology). Here, BSref indicates the climatological BS. The BSS of a perfect forecast is 1. BSS > 0 indicates an improvement over the climatological forecast, BSS = 0 indicates no higher skill than the climatological forecast, and BSS < 0 indicates lower skill than the climatological forecast.

Sample reliability diagram. Red lines show reliability and green bars show forecast frequency.

Appendix

Accessing the hindcast dataset

• The details of past forecasts can be verified and analyzed using the TCC hindcast dataset available online at https://ds.data.jma.go.jp/tcc/tcc/gpv/index.html (access exclusive to registered NMHSs). See Registration information for details.

Akaike's Information Criterion (AIC)

• Akaike's Information Criterion (AIC) (Akaike 1974) is a refined technique based on in-sample fitting to enable estimation of the likelihood that a model will predict future values. The optimal among numerous models is the one with the lowest AIC value.
• Finding the predictor combination with the smallest AIC value enables superior multi-regression modeling.
• The following equation is used to estimate the regression model AIC:
  
  
  
  Here, N denotes sample size, p is the number of the predictor elements, S_e is the residual sum of squares.

References

• Akaike, H., 1974: A new look at the statistical model identification, IEEE Transactions on Automatic Control, 19, 716-723.
• Bishop, C. M., 2006: Pattern recognition and machine learning, Springer.